Ils se trompent, à moins d’avoir été mal compris. Extraits de la TdG du 3 février 2022, articles signés par Monsieur Marc Moulin.
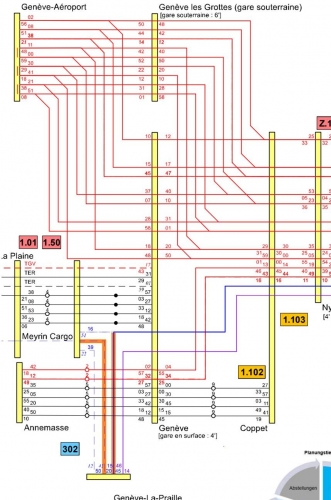
« La retouche majeure porte sur la mise à deux voies, au lieu d’une seule, du tunnel qui raccordera l’aéroport à la future gare souterraine – un quai central à deux voies, niché 17 mètres sous la place de Montbrillant. … On revient donc au plan initial d’un tunnel bidirectionnel, … ».
« Selon les CFF, la capacité des deux voies souterraines – poussée au maximum – atteindrait 24 trains par heure, soit l’arrivée d’un train dans chaque sens toutes les cinq minutes. … ».
La retouche aurait donc pour résultat un nouveau tronçon ferroviaire à double voie, se branchant à l’est sur la ligne de Lausanne à la hauteur du Jardin Botanique et à l’ouest sur la ligne de l’aéroport à hauteur de la bifurcation de Châtelaine, entièrement en souterrain, suivant le tracé actuel ; à la hauteur de Cornavin, les deux voies de la double voie s’écartent l’une de l’autre pour installer un quai.
Tous les trains empruntant ce nouveau tronçon feront halte à Cornavin bien sûr. Ils n’y disposent que d’une voie par sens. Toute gare raisonnable disposerait de deux voies par sens, pour que la capacité en gare soit égale à la capacité en pleine voie. En prétendant que la capacité de chacune des deux voies serait de 12 trains par heure, les CFF se trompent grossièrement : la capacité de ce tronçon ferroviaire nouveau est déterminée par celle de la demi-gare, elle est de l’ordre de 12 trains par heure, 6 par sens.
Le nouveau tronçon ferroviaire ne soulagera pas le réseau en surface de 24 trains par heure (12 par sens) mais de 12 seulement (6 par sens)
Pour pleinement exploiter le tronçon nouveau, il faudrait – il faudra – par la suite réaliser la seconde moitié de cette gare, en ajoutant un second quai et deux voies supplémentaires. Ainsi, contrairement à ce que laisse entendre l’article de Monsieur Moulin, (« dévoilé à huis clos mardi soir à des élus du Canton et de la Ville de Genève, le projet révisé de la gare souterraine de Cornavin promet d’éviter des travaux à répétition »), le projet révisé de la gare souterraine de Cornavin promet un second chantier d’un milliard, au même endroit, le long de l’actuelle voie 8.
La diamétrale voulue par le canton pour permettre l’accès direct du trafic régional à l’aéroport, composée fondamentalement par une nouvelle gare à l’aéroport et un tronçon ferroviaire nouveau reliant cette nouvelle gare à Cornavin via les Nations nécessitera – nécessiterait – absolument la réalisation de la seconde étape d’extension de la gare souterraine de Cornavin.
Qu’on se le dise aux Grottes ! Questionnez vos élus, êtes-vous vraiment sûrs qu’il n’y aura pas un second gigantesque chantier provoquant une seconde fois le chaos quelques années après le 1er. Je dispose d’un texte anonyme, mais issu de l’administration cantonale, qui déclare ceci : « L’affirmation suivante : Il y a la gare proprement dite avec la création de deux voies supplémentaires en souterrain et une préconfiguration pour permettre une extension à 4 voies pour les générations futures n'est absolument pas remise en question. Tout au plus, la solution 1-bis permet de repousser à un horizon encore plus lointain cette deuxième étape ». (IP 160.53.250.80, 10 mars 2022)